EmilyMiller
Ms. Carpenter’s GF
- Joined
- Aug 13, 2022
- Posts
- 14,582
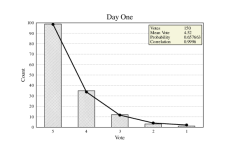
I don’t need to do that. As I explained I know the individual votes on dozens of my stories. They all are J curves, which is precisely what you’d expect given a 1 - 5 rating system.If you want, you can calculate a distribution that might describe your votes, as long as you don't have a low number of votes or any of the other things that cause patterns to deviate.
How did @8letters determine the actual votes cast given the numbers? Or did he fit them to a curve, like @Duleigh?
OK - I’ve read what you said again. The above is NOT an analysis of the actual votes, it’s an exercise in curve fitting. I’m talking about actual vote values captured one by one in low traffic categories. That’s a totally different approach.
Last edited: