Duleigh
Just an old dog
- Joined
- Dec 12, 2004
- Posts
- 6,796
We don't get access to the data other than the story stats that are handed out to us... How many 5 star votes? How many 1 bombs? We may never know unless we sit there refreshing the screen every 5 minutes. I took this issue to a numbers kind of guy who said the same thing I said - you're not going to be able to figure out the vote distribution unless you actually see the vote come in. He said, "Fortunately there's a system that's used by Amazon's rating analytics, Goodreads' Bayesian smoothing (what ever that is) and YouTube's rating estimators, it's called the TLAR system."
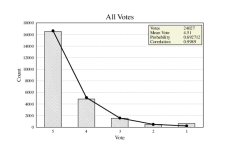
It produces realistic, Stable, Human-like ratings distributions. It's not your exact ratings, but it's a realistic spread. A baseline distribution typical for fiction:
5 70%
70%
4 20%
20%
3 7%
7%
2 2%
2%
1 1%
1%
We just force excel to run these numbers into your actual score and this is what it looks like:

Are these votes right? Probably not, but they're close enough to add up, so who's to say it's wrong? It takes ten calculations per line to get the first one right but then it's all copy paste until you get the worksheet set up.
Cell A2 Story Title
Cell B2 Number of votes cast
Cell C2 Story score
Cell D2 =0.70 + (C2 - 4.55)*0.40 ***(This generates 5 star percentage)
Cell E2 =0.20 - (C2 - 4.55)*0.30 ***(This generates 4 star percentage)
Cell F2 =0.07 - (C2 - 4.55)*0.07 ***(This generates 3 star percentage)
Cell G2 =0.02 - (C2 - 4.55)*0.02 ***(This generates 2 star percentage)
Cell H2 =0.01 - (C2 - 4.55)*0.01 ***(This generates 1 star percentage)
Cell I2 =ROUND(D2 * B2, 0) ***(This concerts the data from Cell D2 to count of 5 Stars)
Cell J2 =ROUND(E2 * B2, 0) ***(This concerts the data from Cell E2 to count of 4 Stars)
Cell K2 =ROUND(F2 * B2, 0) ***(This concerts the data from Cell F2 to count of 3 Stars)
Cell L2 =ROUND(G2 * B2, 0) ***(This concerts the data from Cell G2 to count of 2 Stars)
Cell M2 =ROUND(H2 * B2, 0) ***(This concerts the data from Cell H2 to count of 1 Stars)
You get 5 cells of ugly numbers followed by 5 cells of what you vote count probably is. I hide Columns D through H so it's not so ugly.
And that's it, the TLAR method
TLAR stands for That Looks About Right and that's pretty much what analytics is.
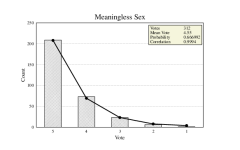
It produces realistic, Stable, Human-like ratings distributions. It's not your exact ratings, but it's a realistic spread. A baseline distribution typical for fiction:
5
4
3
2
1
We just force excel to run these numbers into your actual score and this is what it looks like:

Are these votes right? Probably not, but they're close enough to add up, so who's to say it's wrong? It takes ten calculations per line to get the first one right but then it's all copy paste until you get the worksheet set up.
Cell A2 Story Title
Cell B2 Number of votes cast
Cell C2 Story score
Cell D2 =0.70 + (C2 - 4.55)*0.40 ***(This generates 5 star percentage)
Cell E2 =0.20 - (C2 - 4.55)*0.30 ***(This generates 4 star percentage)
Cell F2 =0.07 - (C2 - 4.55)*0.07 ***(This generates 3 star percentage)
Cell G2 =0.02 - (C2 - 4.55)*0.02 ***(This generates 2 star percentage)
Cell H2 =0.01 - (C2 - 4.55)*0.01 ***(This generates 1 star percentage)
Cell I2 =ROUND(D2 * B2, 0) ***(This concerts the data from Cell D2 to count of 5 Stars)
Cell J2 =ROUND(E2 * B2, 0) ***(This concerts the data from Cell E2 to count of 4 Stars)
Cell K2 =ROUND(F2 * B2, 0) ***(This concerts the data from Cell F2 to count of 3 Stars)
Cell L2 =ROUND(G2 * B2, 0) ***(This concerts the data from Cell G2 to count of 2 Stars)
Cell M2 =ROUND(H2 * B2, 0) ***(This concerts the data from Cell H2 to count of 1 Stars)
You get 5 cells of ugly numbers followed by 5 cells of what you vote count probably is. I hide Columns D through H so it's not so ugly.
And that's it, the TLAR method
TLAR stands for That Looks About Right and that's pretty much what analytics is.